色谱分析中的几大误解
1、误解1:所见即所有(检测器的原理不同,不同检测器对不同化合物响应其实是不同的)
色谱分析时常常有人问,为什么我的仪器走了一些样品后,仪器会污染呢,这种其实也比较好理解,无论如何进行样品前处,我们关注的成分毕竟是少数,提取的样品中必然还会有一个样品组成不是我们的目标分析成分,另外,有些检测器的响应信号是有选择性的,并非没有响应的出峰,就代表提取的待测样品里不含有其他的组成。所以,污染的可能性不光来自一些残留较强的待测组,也来自于那些看不到或者忽视的组分。很多人对于这一点认识不够,会认为,仪器其他检测器进样没有问题,这个检测器一直有问题,就一定是检测器的问题,通常对于能测出杂峰的检测器,说明检测器是灵敏度好的,能测出杂峰,有可能要先检查之前的进样系统,及色谱柱中是否有问题。
2、误解2:谱库是“万能”的,任何成分都可以准确定性
气质联用仪器,通常会配有Nist库,使用Nist库去匹配化合物,是一种常用的技术手段,不过,通常大家会忽略Nist库等谱库匹配技术的一些限制,认为谱库是“万能”的,但常常检索结果会事与愿违,我们不能光要看到谱库检索技术一些优点,方便,快速,相对准确等,但谱库也有以下局限性:
1)、不是所有气质采集的质谱数据都适合检索,一定是全扫描(SCAN)的质谱图适合检索,全扫的检索离子扫描范围不能太窄;选择性离子(SIM)扫描的质谱数据,因采集的质谱是方法限定的几个离子,不具备一个化合物尽可能多的离子碎片信息,不适合用于定性检索识别化合物,可以类似我们人类的指纹,如果是一个图案完整的指纹,在指纹匹配库里就容易匹配上,如果是部分或者不完整的指纹信息,相对不太容易匹配,SIM数据就类似于残破的指纹信息,不适合去用来定性检索匹配的;
2)、采集的质谱图质量差导致检索匹配度差,最理想的是质谱应该与Nist库的测试用的标准品纯度及仪器条件,状态尽可能一致,才能保证采集的质谱图检索匹配度高,而往往由于样品的复杂性,基质的干扰,成分的含量多少(浓度太低的样品, 质谱碎片离子的响应低, 响应太低了,相对丰度会受到的干扰也越大),仪器的状态等种种因素,每个实验室采集的样本的质谱图数据的质量并不能时刻保持一致,因此,匹配分数的多少,不能完全做为化合物定性的参考依据,应该根样品的特性和测试经验(使用单标样品单独采集对比,加标验证等方式)来综合来分析定性;
3)、Nist库收录的化合物并不是无限的,虽然Nist等库每3年都会更新一次,收录的数据在不断增加,不过,也是有限的,很有可能样品中有些成分,Nist这类商业库并示收录。因此,那些想仅靠谱库检索匹配来定性所有未知峰的想法,可以认为是有些“天真”的, 可以这么去想, Nist库对于已经收录的化合物, 对于我们搜寻或匹配化合物,最大的帮助是缩小可能性的范围, 不致于我们“大海捞针”, 盲目猜想, 对于一些常见,常规的化合物还是有很大辅助定性的作用。
3、误解3:气相的响应或灵敏度只要操作方法条件不变,就不会发生改
仪器的方法条件是受仪器的控制单位,如压力或流量控制单元,温度控制单元,这些在仪器没有发生故障的时候,理论上稳定的相同的样品的结果是相对不变的,不过,随着仪器做的样品的增多,样品中那些对检测器来说响应不高或者无响应的复杂的成分,可能在仪器的流路中沉积,这些,样品不断不断地进,有些流路会脏,有些密封垫比如隔垫会污染或被进样针扎漏,其实系统一直在发生着变化的,并非像大多少操作人员想的,我也没有动过什么地方,方法条件也没有变,为什么仪器的响应或灵敏度越来越差。这个是仪器分析最大的误解,样品不断在仪器的流路中过,这个过程本身就是最大的变量,现在没有一家仪器或耗材厂家,敢做这样保证,无法这个世界上任何样品,都不需要更换仪器流路中的消耗品,想要结果尽可能的准确,除了保证方法条件在硬件控制单元的稳定控制,还要保证尽可用干净稳定消耗品。
4、误解4:线性方程内的任意范围都应该是准确的
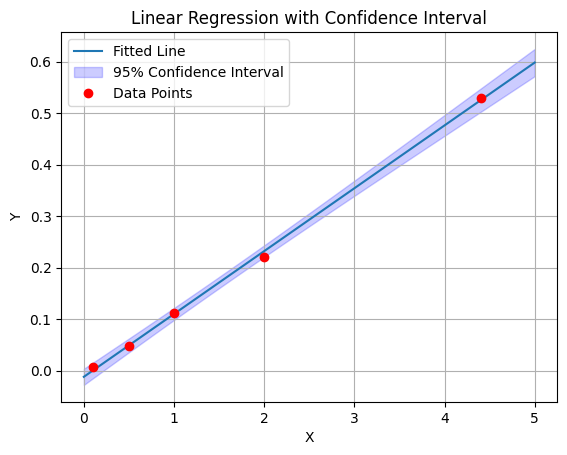
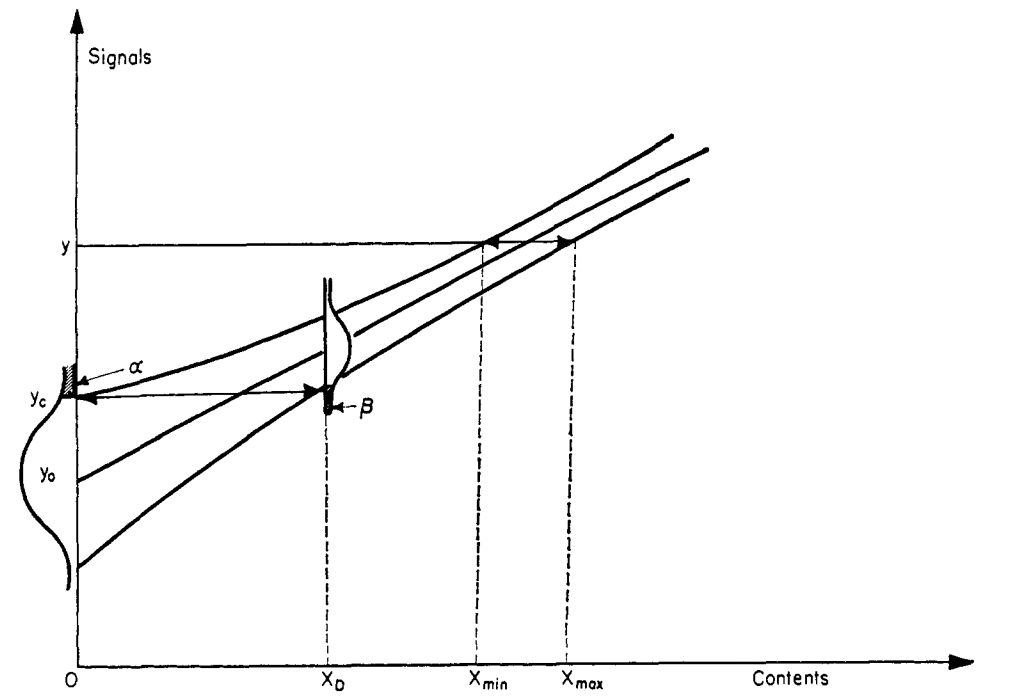
通过配制一系列标准浓度点,绘制一条标准曲线,通过最小二乘法拟合的线性方程,方程在标准浓度点范围内的都应该是准确的,这个也是一个比较容易忽略的误解,如果对最小二乘法的统计公式有深入了解的话,我们会知道,方程在标准浓度低浓点的范围和高浓度点的精度是相对比较差的。可以参考以下图示及python代码示例的验证。
import matplotlib.pyplot as plt
import numpy as np
# Define x and y data points
x = np.array([1/10, 5/10, 10/10, 20/10, 44/10])
y = np.array([
428175 / 57909837,
2710130 / 56207187,
6194034 / 55645431,
12974272 / 58991967,
27660821 / 52149091
])
# Generate x values for plotting the regression line
x_i = np.linspace(0, 5, 300)
# Perform linear regression using polyfit
a, b = np.polyfit(x, y, deg=1)
y_est = a * x_i + b
# Calculate predicted y values for original x
y_pred = a * x + b
# Calculate residuals and standard error
residuals = y - y_pred
SE = np.sqrt(np.sum(residuals**2) / (len(x) - 2))
# Calculate confidence interval
mean_x = np.mean(x)
n = len(x)
t_value = 2.776 # t-distribution value for 95% CI with df = n-2 = 3
conf_interval = t_value * SE * np.sqrt(1/n + (x_i - mean_x)**2 / np.sum((x - mean_x)**2))
# Plotting
fig, ax = plt.subplots()
ax.plot(x_i, y_est, '-', label='Fitted Line')
ax.fill_between(x_i, y_est - conf_interval, y_est + conf_interval, color='blue', alpha=0.2, label='95% Confidence Interval')
ax.plot(x, y, 'o', color='red', label='Data Points')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.legend()
plt.title('Linear Regression with Confidence Interval')
plt.grid(True)
plt.show()